A review of smoothing transforms in WarpLib

For some time series, the exact values of each data point is not always useful, but the general trend is. In that case, a smoothing transform can help better capture the interesting patterns, while removing unwanted irregularities.

Smoothing transforms can be used to produce better visualizations. To some extent, they can also be helpful in removing statistical outliers and detecting anomalies. They can also be used to forecast future values by extrapolating the smoothing model.

In this post, we will review a few options that are available off-the-shelf in WarpLib. WarpLib is the core library of functions that can be leveraged from either WarpScript or FLoWS.

Moving average

The most common function used for smoothing data is the moving average. The function that will compute it is mapper.mean. It can be applied using the MAP framework as below:

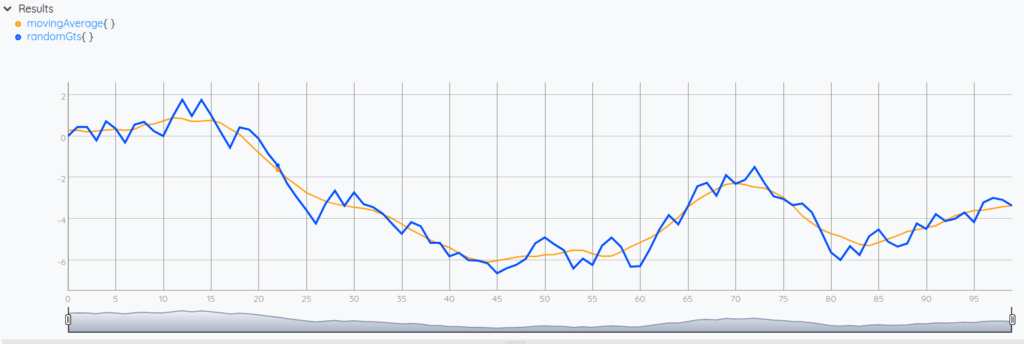
As you can see in the picture above, the blue line has been smoothed out into the orange one.

This can be done for a variety of reasons. One reason often overlooked is that the MAP framework can be used as an alternative to BUCKETIZE for subsampling data. To do this, the 6th argument of MAP (the step, or the number of ticks the moving window moves between each computation) needs to be greater than 1. Aggregates with MAP are then computed with overlapping windows rather than separated buckets like for BUCKETIZE.

Another common usage of the computation of the moving mean is to pinpoint values that deviate too much from it. This is one of the numerous methods used for detecting anomalies. Also, it can be used as part of a technical indicator in monitoring solutions.

Locally weighted regression and scatterplot smoothing

A popular technique that comes from the statistical domain is smoothing by using local weights. That is, the smoother value of each data point are computed using a weighted aggregation of neighboring values, the closer the neighbor, the larger the weight.

In WarpLib, the LOWESS function does that, the regression of the weights is done linearly using the least square method.

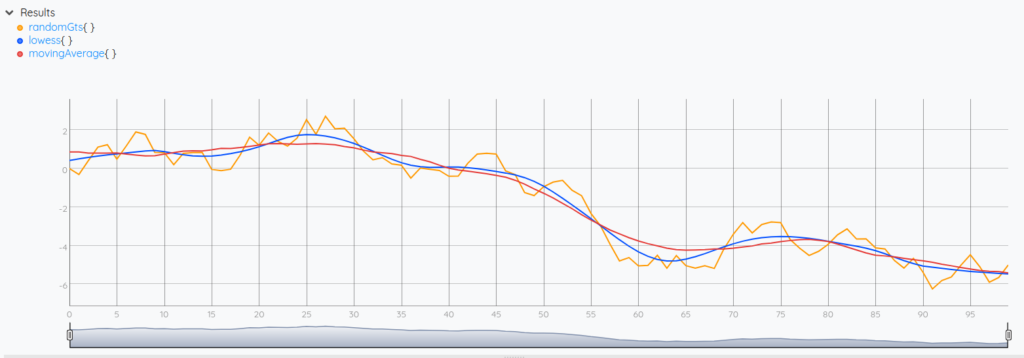
We have plotted the results of a moving average smoothing, and of a lowess smoothing, both using windows of 19 values (for MAP the windows contain the current tick plus the 9 previous and the 9 next ticks; for LOWESS we take the 19 closest ticks which end up forming the same windows of values). If you look carefully, the lowess plot is closer to the original values.

Robust smoothing

Sometimes, there are values that are there by mistake or are just anomalies.

In the smoothing process, it would be wise not to use them to compute the smoother values during the aggregation, or else their impact would be seen on the result. If you can detect the aberrant values, fine. Detect them, remove them, and then smooth out the data.

But what if it's not that easy to detect them? What if you don't have the time to run an additional step for detecting outliers? In that case, you can make use of robust smoothing transforms, which would negate the effect of outliers on your smoothing. In WarpLib, you can use the function RLOWESS, which is in fact a version of LOWESS that is robust to outliers.

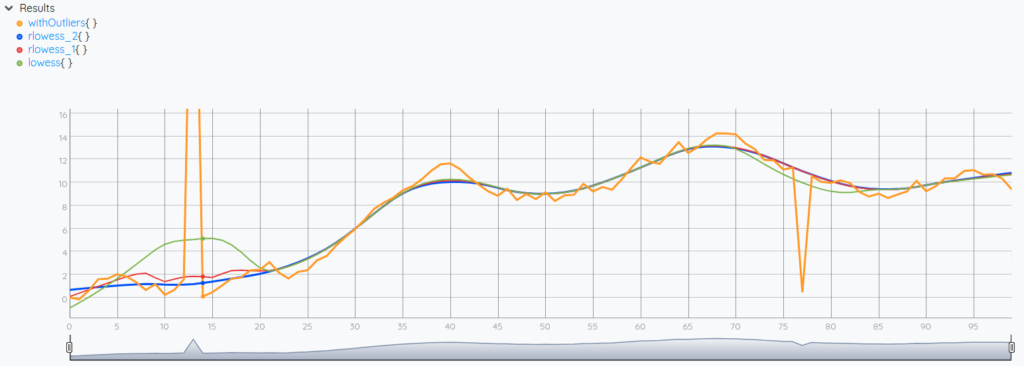
On the script above, we have generated a random walk series in which we have inserted aberrant values at tick 13 and tick 77 (orange line). Then, we applied a lowess smoothing (green line), a 1-rlowess smoothing with 1 robustifying iteration (red line), and a 2-rlowess smoothing with 2 robustifying iteration (blue line).

As we can see in the results, the lowess smoothing is hugely impacted by both aberrations. The 1-rlowess is still impacted on the first one, but the 2-rlowess seems not. Usually, setting the second parameter to 2 (number of robustifying iterations) is enough to get rid of the affect of outliers.

Additionally, RLOWESS is not just better than LOWESS for handling outliers, it can also produce faster and better smoothing. The third parameter is a number of ticks to jump between each regression to speed up the process. The fourth parameter is the polynomial degree of the smoothing kernel, allowing for producing smoother lines.

Exponential smoothing

Exponential smoothing usually refers to smoothing algorithms that compute the weighted aggregations of all past values to compute the smoother value at a particular tick, where the weights are exponentially decreasing the further we go back in the past.

In the core WarpLib library, there are two types of exponential smoothing that are implemented: SINGLEEXPONENTIALSMOOTHING and DOUBLEEXPONENTIALSMOOTHING. If you are curious, you can read the explanations in the documentation, and get more details on this Wikipedia article. Set their parameters close to 1 if you want the result to be more dependent on recent values, and closer to 0 if you want a smoother result.

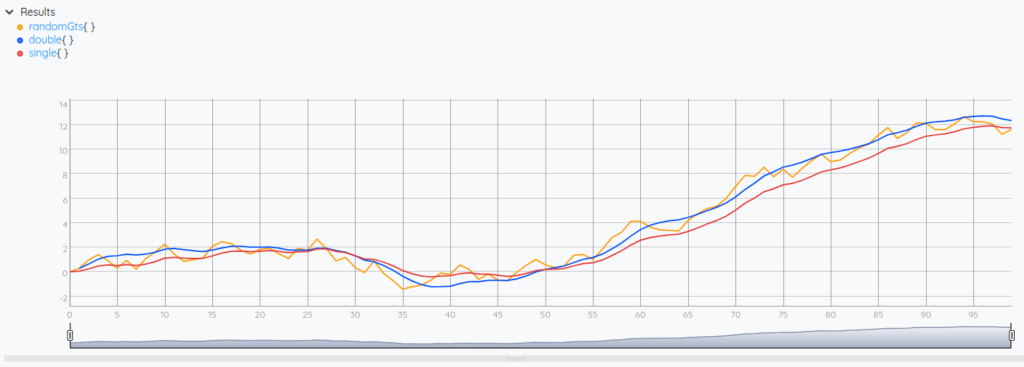
On the result above, we can see that the single exponential smoothing fails at capturing the trend of the data toward the end of the curve, compared to the result of the double exponential smoothing.

It's worthy to note that exponential smoothing methods are also commonly used for producing forecasts. The forecast extension contains additional forecast functions and some of them are based on exponential smoothing methods.

Smoothing kernels

Last but not least, there is also a family of kernels implemented within the MAP framework. They can be used to compute distances in some situations and be relevant in some specific cases to be used as smoothing kernels. We won't go into the specifics for these functions because they are for advanced usages:

• mapper.kernel.cosine
• mapper.kernel.epanechnikov
• mapper.kernel.gaussian
• mapper.kernel.logistic
• mapper.kernel.quartic
• mapper.kernel.silverman
• mapper.kernel.triangular
• mapper.kernel.tricube
• mapper.kernel.triweight
• mapper.kernel.uniform

It's nice to know that these kernels are implemented for the day you would need them. Note that there is also mapper.dotproduct if you need a kernel with custom discrete weights.

Conclusion

In this blog post, we have seen numerous functions from WarpLib that can be used to smooth out data.

Among them are mapper functions, to compute moving averages, or to apply a smoothing kernel on a moving window. The RLOWESS function implements locally weighted regression that can be robust to outliers, with some options to make it faster and/or smoother. LOWESS is a particular case of RLOWESS. It is equivalent to q 0 0 1 RLOWESS (no robustness, no acceleration, regression is linear).

Exponential smoothing functions, including SINGLEEXPONENTIALSMOOTHING and DOUBLEEXPONENTIALSMOOTHING can be used when we want all past values to affect the smoothing, rather than just values within a fixed-sized window. The latter function is favored when the data is trended.

Also, it's also nice to keep in mind that all these functions can be used for other means, including anomaly detection and forecasting.

I hope that this article made you discover more WarpLib functions. Until next time, happy smoothing, and explore all the Warp 10 capabilities with the blog!

Jean-Charles Vialatte

Machine Learning Engineer